Einführung

Der Begriff "Exotische Derivate" ist etwas schwammig. Wenn man etwas mit dem Wort "exotisch" beschreibt, dann drückt man eigentlich aus, dass etwas "positiv fremdartig" ist. Im Fall von Derivaten meint man eigentlich, dass die Auszahlungsfunktionen eine gewisse Komplexität aufweisen. Die Welt der exotischen Derivate ist dementsprechend vielfältig und wir werden hier nur einen winzigen Ausschnitt dieser weiten Welt betrachten können (wohlgemerkt nur im CRR-Modell). Streng genommen haben wir in <a href="{url 'blogContent' 7}">Teil 3: Pricing von Derivaten</a> bereits exotische Derivate kennengelernt (u.a. binäre Optionen). Wir werden uns hier speziell einem Derivat widmen, deren Auszahlung vom maximalen Preis eines Wertpapieres abhängt. Das Pricing solch eines Derivates ist deutlich komplizierter und wir benötigen ein neues Werkzeug.

Irrfahrt

Das Hilfsmittel, welches wir benötigen, basiert auf dem sogenannten Reflexionsprinzip. Das Reflexionsprinzip wird uns bei der konkreten Berechnung von einigen exotischen Derivaten unterstützen. Wir stellen uns eine Zufallsvariable vor, welche die Anzahl der "Ups" und "Downs" zählt. Das ganze geschieht wie folgt. Wir starten zum Zeitpunkt 0 beim Wert 0. Hat man zum Zeitpunkt 1 einen "Up" so zählen wir eine 1 dazu. Haben wir einen "Down" eine -1. Auf diese Weise erhalten wir eine sogenannte "Irrfahrt". Die folgende Abbildung zeigt vier mögliche Realisierungen einer Irrfahrt, wenn die Wahrscheinlichkeit für einen "Up" und "Down" zu jedem Zeitpunkt gleich ist. Solche Irrfahrten kann man auf vielerlei interessante Eigenschaften untersuchen, z.B. ob die Irrfahrt mal einen zurückliegenden Zustand wieder erreicht.

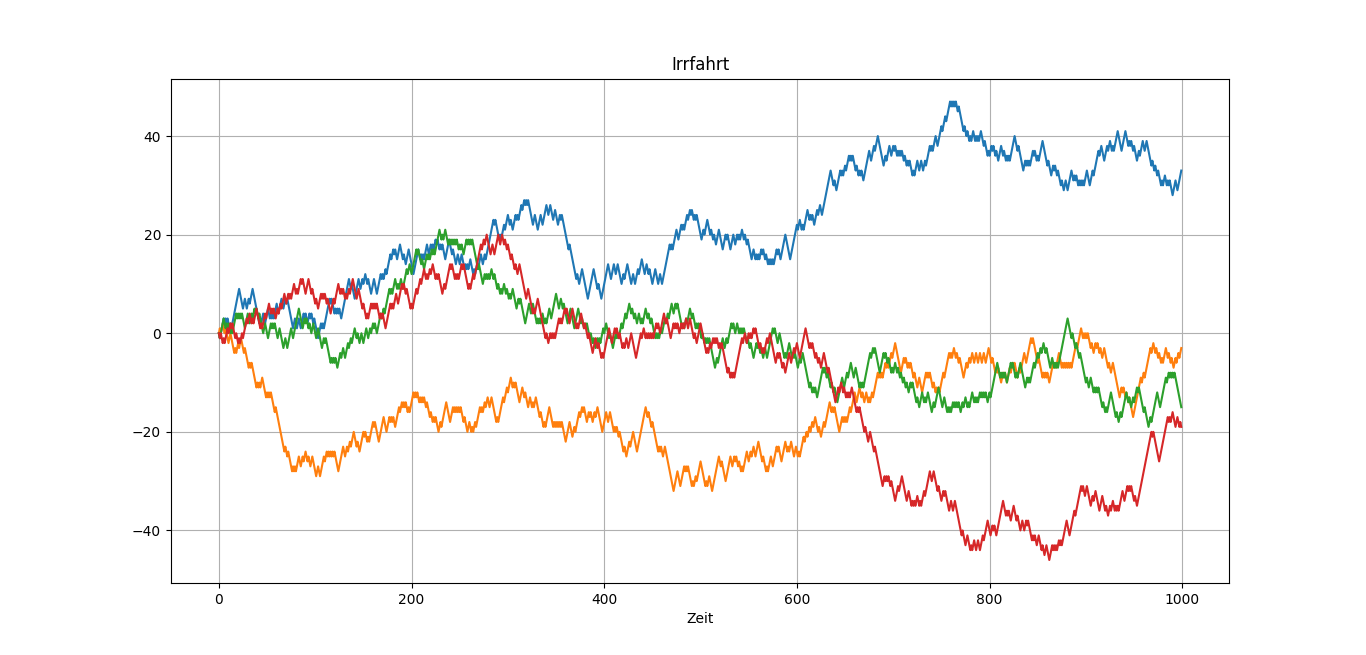
Es folgt nun eine etwas formalere Definition. Es sei für jedes \( Y_t \) die Wahrscheinlichkeit \( \mathbb{P}[Y_t = 1] \in (0,1) \) konstant und \( \mathbb{P}[Y_t = -1] = 1 - \mathbb{P}[Y_t = 1] \). Dann bezeichnet man den Prozess mit \( Z_0 := 0 \) und \( Z_t := \sum_{j = 0}^{t} Y_j \) als Irrfahrt. Für unser eindeutiges Martingalmaß \( \mathbb{P}^{\star} \) (im CRR-Modell) gilt

\[ \mathbb{P}^{\star}[ \{\max\limits_{0 \leq t \leq T} Z_t \geq k\} \cap \{ Z_T = k - l \}] = (\frac{1-p^{\star}}{p^{\star}})^l \cdot \mathbb{P}^{\star}[ Z_T = k + l ] \]

\[ = (\frac{p^{\star}}{1 - p^{\star}})^k \cdot \mathbb{P}^{\star}[ Z_T = -k - l ] \]

Diese Gesetzmäßigkeit folgt direkt aus dem Reflexionsprinzip, welches an dieser Stelle nicht näher erläutert wird, da es dem Ziel dieses Textes nicht gerecht werden würde (dem interessierten Leser empfehle ich hier das Buch STOCHASTIC FINANCE, AN INTRODUCTION IN DISCRETE TIME von Hans Föllmer und Alexander Schied). Kommen wir zur Praxis.

Up-and-in Call Option

Wir definieren ein Derivat mit der Auszahlung \( C_{UI} := (S_T - K)^+ \cdot \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} } \) mit einen Strike \( K > 0 \) und \( B > \max \{ S_0,K \} \) als Up and in Call Option. Wie verhält sich dieses Derivat? Der zugehörige Basiswert muss erstmal eine sogenannte Barriere \( B \) durchbrechen, bevor der Investor eine Chance auf eine Auszahlung hat (also ein Käufer). Wir müssen ein paar weitere Einschränkungen machen, um den Preis berechnen zu können. Zum einen sei im folgenden \( 1 + r_{down} = \frac{1}{1 + r_{up}} \) und es existiere ein \( k \in \mathbb{N} \) mit \( B = S_0 \cdot (1 + r_{up})^k \). Wir wissen prinzipiell schon wie das Pricing erfolgt. Es gilt

\[ \pi_{UI} = \frac{\mathbb{E}^{\star}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} }]}{(1+r)^T} \]

\[ = \frac{\mathbb{E}^{\star}[(S_T - K)^+ \cdot (\mathbb{1}_{ \{ S_T \geq B \} } + \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} \cap \{ B > S_T \} }) ]}{(1+r)^T} \]

\[ = \frac{\mathbb{E}^{\star}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ S_T \geq B \} } ] + \mathbb{E}^{\star}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} \cap \{ B > S_T \} } ]}{(1+r)^T} \]

Den Summanden \( \mathbb{E}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ S_T \geq B \} } ] \) kann man einfach berechnen. Für den anderen Summanden benötigen wir das bereits angesprochene Reflexionsprinzip. Es gilt

\[ \mathbb{E}^{\star}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} \cap \{ B > S_T \} } ] \]

\[ = \mathbb{E}^{\star}[(S_T - K)^+ \cdot ( \sum_{l \geq 1} \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} Z_t \geq k \} } \cdot \mathbb{1}_{ \{ Z_T = k - l \} } ) ] \]

\[ = \sum_{l \geq 1} \mathbb{E}^{\star}[(S_T - K)^+ \cdot ( \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} Z_t \geq k \} } \cdot \mathbb{1}_{ \{ Z_T = k - l \} } ) ] \]

\[ = \sum_{l \geq 1} (S_0 \cdot (1 + r_{up})^{k - l} - K)^+ \cdot \mathbb{P}^{\star}[ \{ \max\limits_{0 \leq t \leq T} Z_t \geq k \} \cap \{ Z_T = k - l \}] \]

\[ = \sum_{l \geq 1} (S_0 \cdot (1 + r_{up})^{k - l} - K)^+ \cdot (\frac{p^{\star}}{1 - p^{\star}})^k \cdot \mathbb{P}^{\star}[ \{ Z_T = - k - l \}] \]

\[ = (\frac{p^{\star}}{1 - p^{\star}})^k \cdot \sum_{l \geq 1} (1 + r_{up})^{2k} \cdot (S_0 \cdot (1 + r_{up})^{- k - l} - \frac{K}{(1 + r_{up})^{2k}})^+ \cdot \mathbb{P}^{\star}[ \{ Z_T = - k - l \}] \]

\[ = (\frac{p^{\star}}{1 - p^{\star}})^k \cdot (1 + r_{up})^{2k} \cdot \sum_{l \geq 1} (S_0 \cdot (1 + r_{up})^{- k - l} - \frac{K}{(1 + r_{up})^{2k}})^+ \cdot \mathbb{P}^{\star}[ \{ Z_T = - k - l \} ] \]

Wie lässt sich der letzte Ausdruck nun interpretieren? Wenn \( Z_T = - k - l \) ist, gilt auch \( S_T = S_0 \cdot (1 + r_{up})^{-k-l} = S_0 \cdot (1 + r_{up})^{-k} \cdot (1 + r_{up})^{-l} = S_0 \cdot \frac{S_0}{B} \cdot (1 + r_{up})^{-l} = S_0 \cdot \frac{S_0}{B} \cdot (1 + r_{down})^{l} \). Damit gilt auch \( S_T < S_0 \cdot \frac{S_0}{B} \). Schlussendlich gilt also \( \mathbb{E}^{\star}[(S_T - K)^+ \cdot \mathbb{1}_{ \{ \max\limits_{0 \leq t \leq T} S_t \geq B \} \cap \{ B > S_T \} } ] = (\frac{p^{\star}}{1 - p^{\star}})^k \cdot (1 + r_{up})^{2k} \cdot \mathbb{E}^{\star}[ (S_T - \frac{K}{(1 + r_{up})^{2k}})^+ \cdot \mathbb{1}_{ \{ S_0 \cdot \frac{S_0}{B} > S_T \} } ] \)

Der Ausdruck kann problemlos berechnet werden (mittels Binomialverteilung). Sehen wir uns an wie sich der Preis verhält, wenn gewisse Parameter verändert werden. Im folgendem sei der Startpreis eines Assets 1, der Up sei 1 und der down -0.5. Wie 
auch im Artikel <a href="../003_CRR-Modell-Teil-3/crrModellTeil3.html">Das CRR-Modell - Teil 3: Pricing von Derivaten</a> kann das Verhalten des Preises bei Variation von Parametern nicht vollständig betrachtet werden (erst recht nicht bei komplexeren Derivaten).

Der Preis steigt, wie zu erwarten, mit steigender Laufzeit an.

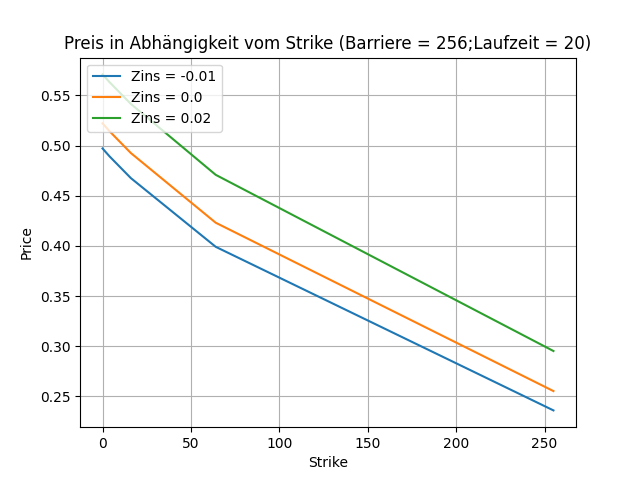
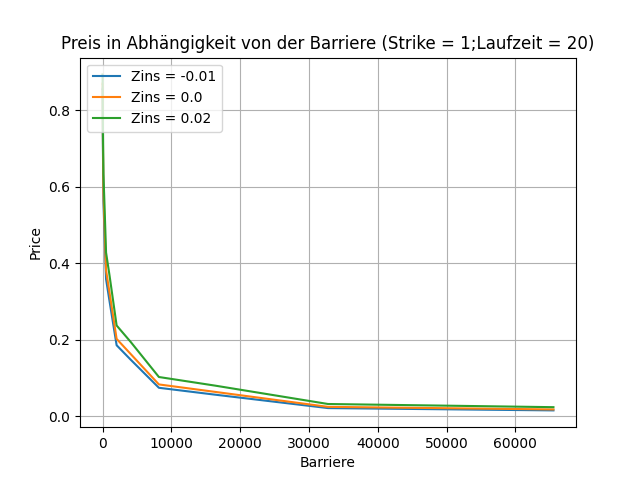
Mit steigendem Strike bzw. steigender Barriere sinkt der Preis (was ebenfalls plausibel ist).

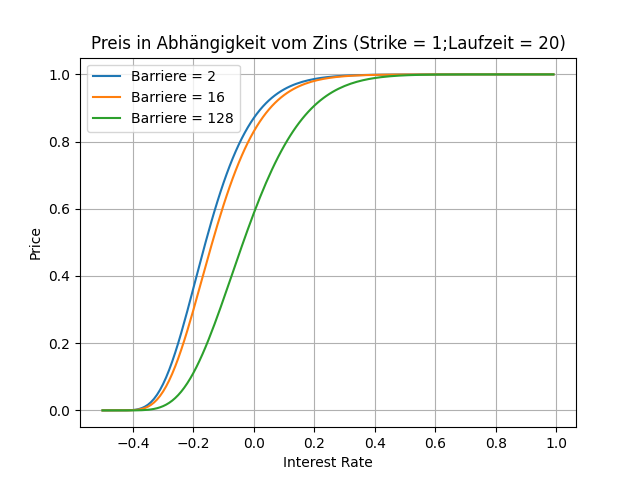
Mit steigenden Zins steigt auch der Preis monoton an, ähnlich wie bei der klassischen europäischen Call Option. Diesen Umstand kann man grundsätzlich hinterfragen, denn bei herkömmlichen Bewertungsverfahren sollte der Preis eines Assets eigentlich sinken, da der Diskontierungsfaktor kleiner wird. Es wirkt aber ein weiterer Effekt. Wird größer, nähert er sich den "Up" Wert an. Damit vergrößert sich die Wahrscheinlichkeit, dass sich der Wert eines Assets zu einem nächsten Zeitpunkt erhöht. Um diesen Umstand auszugleichen, muss der faire Preis auch höher werden. Alternativ rechne man einfach nach.

Ausblick

Wir haben uns bis jetzt lediglich dem Pricing gewidmet. Wir wollen uns nun endlich dem Hedging widmen. Dazu wird wieder etwas Theorie notwendig sein, bevor wir uns einigen praktischeren Beispielen zuwenden. Anschließend werden wir das bisher gelernte an echten Börsendaten testen und uns mit weiteren praktischen Fragen beschäftigen (beispielsweise die Wahl geeigneter Parameter).