Einführung

Es gelten die gleichen Voraussetzungen, wie in den vorherigen Teilen. Wir wollen uns nun mit Hedging-Strategien beschäftigen. Es geht darum ein Portfolio \( \xi_T \) zu entwickeln, welches \( \bar{S}_T \bar{\xi}_T = C \) immer erfüllt. Es handelt sich also um eine Art Absicherungsstrategie. Es kann viele gute Gründe für so eine Strategie geben. Ein Unternehmen könnte sich z.B. mittels Derivate gegen steigende oder sinkende Rohstoffpreise absichern. Ein Investor könnte seine Aktien z.B. mit einer Option absichern, wenn dieser erwartet, dass diese innerhalb eines bestimmten Zeitraum fallen könnten.

Theorie

Die erste Frage, die im Raum steht, ist, ob es in unserem Marktmodell überhaupt Hedging-Strategien gibt. Zuerst wollen wir nochmal konkretisieren, was wir unter einer Hedging-Strategie verstehen bzw. (präziser) was wir unter Claims verstehen, für die es eine Hedging-Strategie gibt. Ein Claim \( C \) heißt replizierbar, falls es eine eine selbstfinanzierende Strategie \( \bar{\xi} \) gibt (bzw. Hedging- oder Replikationsstrategie), so dass fast sicher \( \bar{S}_T \bar{\xi}_T = C \) gilt. Dabei heißt Selbstfinanzierend, dass stehts die folgende Eigenschaft gil: \( \bar{S}_t \bar{\xi}_t = \bar{S}_t \bar{\xi}_{t+1} \) für alle \( t = 1, \cdots T-1 \). Konkret heißt das, dass ein Investor zu keinem Zeitpunkt weiteres Kapital in das Portfolio steckt.

Für einen gegebenen Claim stellt sich also die Frage, ob dieser replizierbar ist. Tatsächlich ist im CRR-Modell jeder Claim replizierbar. In <a href="../002_CRR-Modell-Teil-2/crrModellTeil2.html">Das CRR-Modell – Teil 2: Arbitragefreiheit und Pricing – SemperInvest</a> wurde bereits angemerkt, dass das arbitragefreie CRR-Modell vollständig ist. Damit ist (technisch gesehen) gemeint, dass es nur ein äquivalentes Martingalmaß in unserem Modell gibt. D.h. auch, dass jeder Contingent Claim nur einen arbitragefreien Preis besitzt. Diese theoretischen Zusammenhänge kann man in STOCHASTIC FINANCE, AN INTRODUCTION IN DISCRETE TIME von Hans Föllmer und Alexander Schied nachlesen.

Auf den ersten Blick scheint das kaum vorstellbar zu sein, dass man mit einem Bond und einer Aktie ein hinreichend komplexes Derivat einfach so "nachbauen" kann. Ich will den Leser hier aber nochmal darauf hinweisen, dass wir von Derivaten der Art \( H = h(S_0, S_1, \cdots, S_T) \) sprechen (zur Erinnerung: \( H = \frac{C}{(1+r)^T} \)). D.h. unser Derivat ist in der Komplexität dahingehend beschränkt, dass es nur von der Wertentwicklung eines Wertpapieres abhängen darf (schließlich gibt es in unserem Modell keine weiteren Wertpapiere --> Möglicherweise ein berechtigter Kritikpunkt an dem Modell).

Anhand einiger Beispiele kann man sich leicht klar machen, dass es eben doch möglich ist. Grund dafür ist die binäre und baumartige Struktur des CRR-Modells. Grundsätzlich kann man sich eine Hedging-Strategie einfach ausrechnen, indem man ein lineares Gleichungssystem löst. Dazu sei im folgendem unser Zins gleich 0, ein Up entspricht 1 und ein Down entspricht - 0.5. Wir betrachten ein zweiperiodisches Modell. Unser risikobehaftetes Asset sei eine Aktie mit einem Startpreis von 100. Wir wollen nun eine Hedging-Strategie für eine europäische Call-Option mit Strike 100 berechnen.

Wir wissen, dass unsere Strategie die oben definierte Bedingung \( \bar{S}_T \bar{\xi}_T = C \) erfüllen muss. Betrachten wir denn Fall, dass unsere Aktie nach der ersten Periode (t = 1) den Wert 200 hat. Zum nächsten Zeitpunkt könnte sich der Wert auf 100 halbieren oder auf 400 verdoppeln. Im ersten Fall hätte unsere Call-Option eine Auszahlung 0, im zweiten Fall dagegen 400 - 100 = 300. D.h. es muss einerseits gelten, dass \( \xi^0_2 + 100 \cdot \xi^1_2 = 0 \) und \( \xi^0_2 + 400 \cdot \xi^1_2 = 300 \). Zieht man nun von der zweiten Gleichung die erste ab, so erhält man, dass \( 300 \cdot \xi^1_2 = 300 \) gilt. Somit gilt \( \xi^1_2 = 1 \). Daraus folgt, dass \( \xi^0_2 + 400 = 300 \), also \( \xi^0_2 = -100 \).

Analog geht man im Fall vor, dass die Aktie nach einer Zeiteinheit den Wert 50 hat. Es gelten die Gleichungen \( \xi^0_2 + 25 \cdot \xi^1_2 = 0 \) und \( \xi^0_2 + 100 \cdot \xi^1_2 = 0 \). Daraus folgt, analog wie eben, \( 75 \cdot \xi^1_2 = 0 \). Damit ist \( \xi^1_2 = 0 \) und somit ist auch \( \xi^0_2 = 0 \).

Man würde analog fortfahren (sozusagen in die Vergangenheit schreiten). Mann kennt nun den Wert des Portfolios zum Zeitpunkt t= 1. Das wäre im ersten Fall \( -100 + 1 \cdot 200 = 100 \) und im zweiten Fall 0. Man löse nun das lineare Gleichungssystem mit \( \xi^0_1 + 50 \cdot \xi^1_1 = 0 \) und \( \xi^0_1 + 200 \cdot \xi^1_1 = 100 \) (die Lösung überlasse ich dem Leser). Man beachte außerdem, dass wir die Bedingung, dass die Strategie selbstfinanzierend sein muss, einhalten.

Bevor wir in den nächsten Abschnitt springen, möchte ich diesen noch mit der eben getätigten Rechnung motivieren. Wie haben wir den Anteil der Aktien, die wir kaufen müssen eigentlich genau berechnet? Wir wissen z.B., dass \( \xi^1_2 = 1 = \frac{300}{300} = \frac{300}{400 - 100} = \frac{300 - 0}{400 - 100} \). Der aufmerksame Leser erkennt nun möglicherweise warum man wir im folgendem von "Delta"-Hedging sprechen werden. Die oben dargestellte Zahl ist eine von mehreren wichtigen Sensitivitätskennzahlen. Wir schauen uns an wie sehr sich der Wert eines Derivats ändert, wenn sich der Preis der Aktie ändert. Man könnte im weitesten Sinne von einer Art Differential sprechen.

Delta-Hedging

Im CRR-Modell müssen wir für jeden Zeitpunkt (und für jedes Szenario) wissen wie viele Anteile von der Aktie bzw. wie viele Anteile vom Bond gekauft werden müssen. Bevor wir zur eigentlichen Berechnung kommen sollte sich der Leser zunächst darüber im klaren sein, dass der Preis für eine Hedging-Strategie zum Zeitpunkt \( t \) genau dem Preis des Contingent Claims zu diesem Zeitpunkt entsprechen muss. Andernfalls gäbe es eine Arbitragegelegenheit. Konkret heißt dies \( \frac{\mathbb{E}^{*}[C\mid \mathcal{F}_t]}{(1+r)^T} = \bar{\xi}_t \cdot \bar{X}_t = \xi^0_t \cdot S^0_t + \xi^1_t \cdot X^1_t \). Kennt der Händler die Menge der Aktien, die er kaufen (bzw. leerverkaufen) muss, um eine Delta-Hedging-Strategie umzusetzen, ist der Anteil des Bonds

\[ \xi^0_t = \frac{\mathbb{E}^{*}[H\mid \mathcal{F}_t] - \xi^1_t \cdot X^1_t}{(1+r)^t}. \]

Für den Anteil der Aktien, die zum Zeitpunkt t-1 gekauft werden müssen, gilt die Formel (wie im vorherigen Abschnitt motiviert)

\[ \xi^1_t = \frac{(1+r)}{x_{t-1}(b - a)} \cdot \mathbb{E}^{*}[h(x_0, x_1, \cdots, x_{t-1}, x_{t-1} \cdot (1+up) \cdot (1 + R_{t+1}), \cdots, x_{t-1} \cdot (1+up) \cdot \prod_{j = t+1}^{T} (1 + R_j) (1 + R_{t+1})) \mid \mathcal{F}_{t-1}] \]

\[ - \mathbb{E}^{*}[h(x_0, x_1, \cdots, x_{t-1}, x_{t-1} \cdot (1+down) \cdot (1 + R_{t+1}), \cdots, x_{t-1}  \cdot (1+down) \cdot \prod_{j = t+1}^{T} (1 + R_j) (1 + R_{t+1})) \mid \mathcal{F}_{t-1}]. \]

Den Beweis Schlage man in STOCHASTIC FINANCE, AN INTRODUCTION IN DISCRETE TIME von Hans Föllmer und Alexander Schied nach. Möglicherweise erschreckt der Leser beim Anblick dieses Termes. Die Werte \( x_0, x_1, \cdots, x_{t-1} \) sind die bereits bekannten Werte, welche die Aktie zu den entsprechenden Zeitpunkten hatte. Im Zähler des Bruchs wird der erwartete (diskontierte) Wert des Claims zum aktuellen Zeitpunkt berechnet (Also unter den gegebenen Voraussetzungen). Dabei wird einmal der Fall angenommen, dass die Aktie steigt oder sinkt.

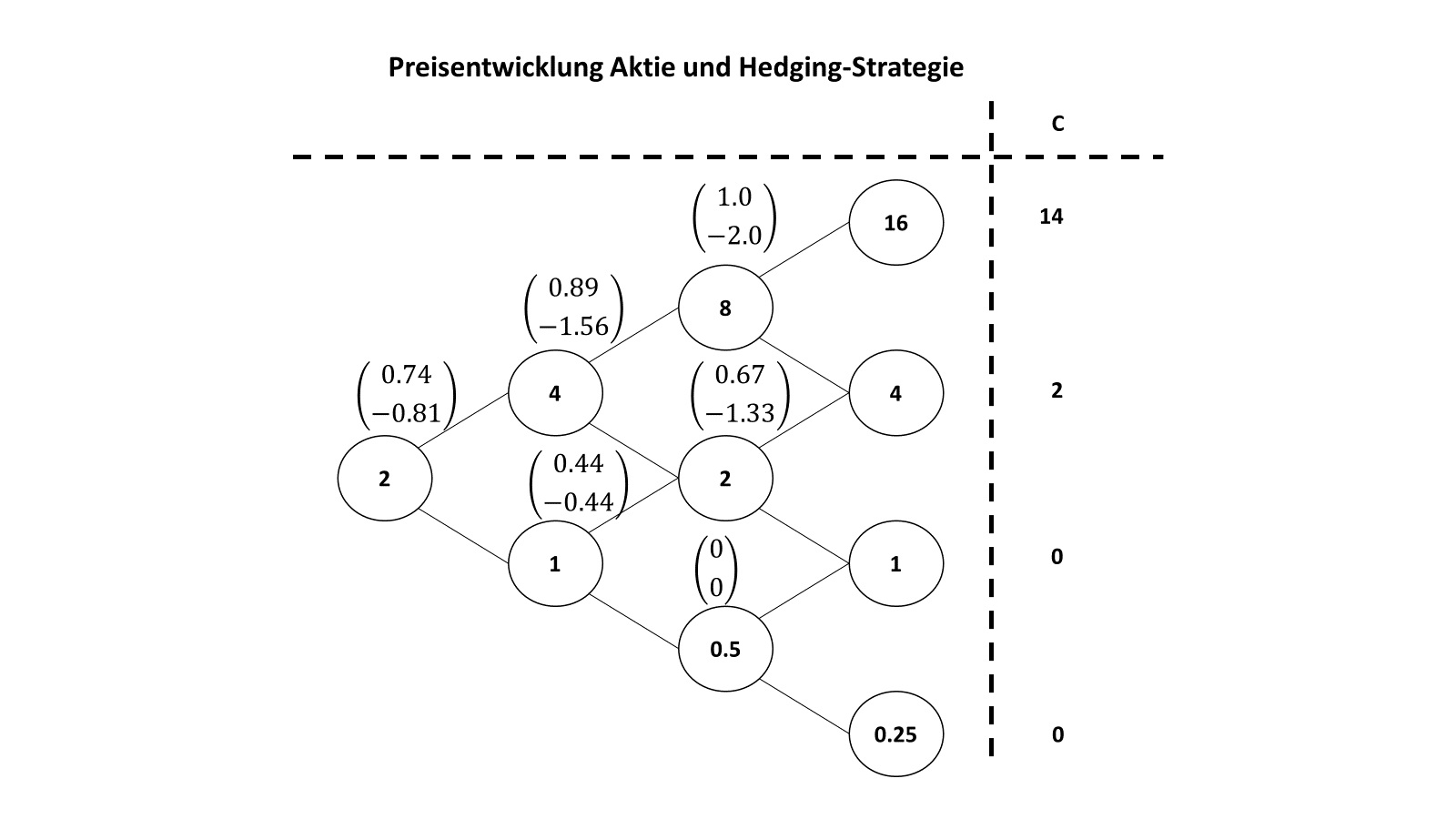
Der Leser überzeuge sich anhand einer eigenen Rechnung selber, dass die obigen Formeln zum gewünschten Ergebnis führen. Dabei seien die Parameter wie folgt gewählt: Das Modell habe 3 Perioden, der Zins sei 0, ein Up entspricht 1, ein Down entspricht - 0.5 und die Aktie starte mit einem Preis von 2. Dazu betrachten wir eine europäische Call-Option mit Strike 2. Die Lösung ist in der folgenden Abbildung.

Fazit

Eigentlich ist spätestens jetzt alles wichtige zum CRR-Modell gesagt. Der Leser sollte nun die Prämissen des Modells kennen, wie man den Wert von Derivaten berechnet und wie man Hedging-Strategien berechnet. Dennoch bleiben vorerst viele Fragen offen. Welchen Zins verwendet man, wie granular wählt man die Zeitabschnitte, wie nutzt man das Modell grundsätzlich, welche Risiken bestehen bei Verwendung des Modells, etc. Die ein oder andere dieser Fragen soll hier zukünftig behandelt werden und somit wird uns das CRR-Modell als möglicherweise einfachstes Modell in der klassischen Finanzmathematik immer wieder begegnen.